Introduction and Prerequisites
In this article we will be discussing about the k-means algorithm for clustering. This is the first in a series of articles related to Machine Learning that I will be writing about in Trends Of Code.
The prerequisites for this article is almost nothing, but if you are completely new to Machine Learning I would recommend you to first build up from an even simpler machine learning algorithm like k-nearest neighbours and get an idea of how a general machine learning algorithm works. Still, I will be building up from the very basics and hence understanding this article without any pre knowledge should also not be difficult.
A very natural follow up to this article would be a more general algorithm, called the Fuzzy c-means (FCM) algorithm, also known as the soft version of k-means. That will probably be the next article that I will write in Trends of Code. Also, as a note, I have introduced a vertical scroll view too since the previous post reported lack of support for some browsers.
The prerequisites for this article is almost nothing, but if you are completely new to Machine Learning I would recommend you to first build up from an even simpler machine learning algorithm like k-nearest neighbours and get an idea of how a general machine learning algorithm works. Still, I will be building up from the very basics and hence understanding this article without any pre knowledge should also not be difficult.
A very natural follow up to this article would be a more general algorithm, called the Fuzzy c-means (FCM) algorithm, also known as the soft version of k-means. That will probably be the next article that I will write in Trends of Code. Also, as a note, I have introduced a vertical scroll view too since the previous post reported lack of support for some browsers.
What is Clustering?
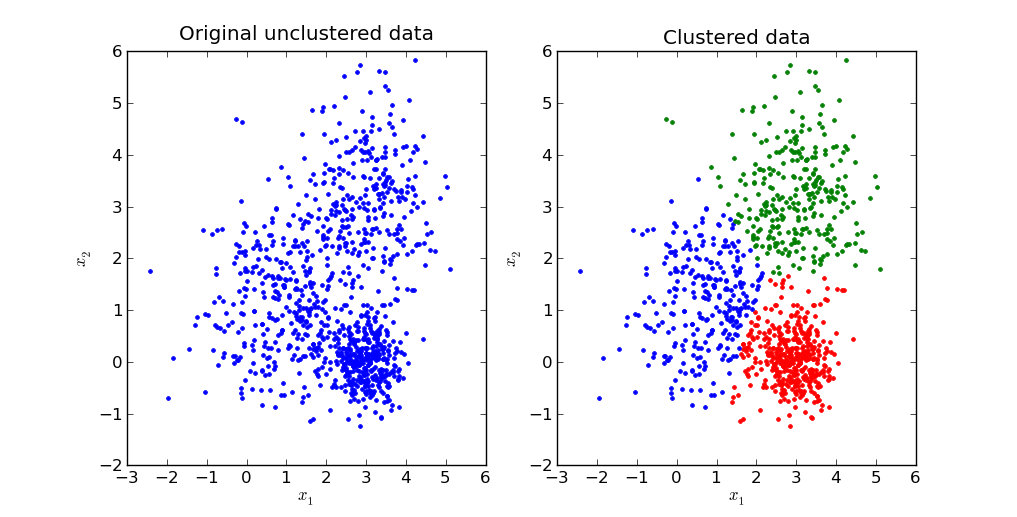
Most of the readers would probably skip this section, but now that we are in, let’s give you something to take back. In any machine learning problem we have data (i.e. training data). Clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense or another) to each other than to those in other groups (clusters). Clustering is a type of unsupervised learning problem; it essentially means that the data that we have is not labeled, i.e. we don’t know which data point belongs to which cluster. If we had known that, the problem gets transformed into a classification problem. There are various approaches (or solutions, as you may like it to call) to the clustering problem. In general, there are two major classes that many of the algorithms belong to: Partitioning Relocation Clustering and Hierarchical Clustering. The k-means belongs to partition relocation type of algorithms. Clustering is an extremely important problem and the applications are huge. Visit the wikipedia reference [1] to explore the applications. We will now proceed to the next section, I think the problem statement is pretty self explanatory. You will get a better feel as we proceed in the article.
The K-Means Algorithm
The term "k-means" was first used by James MacQueen in 1967 though the idea goes back to Hugo Steinhaus in 1957. If you have anything to do with machine learning or data science, you should know the k-means algorithm. It is one of the most simple and at the same time one of the most famous algorithms.
Goal
K-Means clustering aims to partition the observations into clusters in which each input data point belongs to the cluster with the nearest mean, serving as a prototype of the cluster.
The problem is NP-hard, but there are efficient heuristic algorithms that are commonly employed and converge quickly to a local optimum.
The problem is NP-hard, but there are efficient heuristic algorithms that are commonly employed and converge quickly to a local optimum.
Input
We have a set of feature vectors which serve as data points. Hence we have xi∈RD, where D is the feature space cardinality and i can range from 1 to N where N is the number of data points. We have to assign all these N data points to some k clusters.

Objective Function Formulation
Let 𝜇𝑘 ∈ 𝑅𝐷 be the center of cluster k, thus serving the prototype for kth cluster.
Let 𝛾 be the indicator variables for the cluster assignment, such that:
𝛾𝑛𝑘 =1 if 𝑥𝑛 belongs to 𝑘
𝛾𝑛𝑘 = 0 else
The objective is then the minimization of
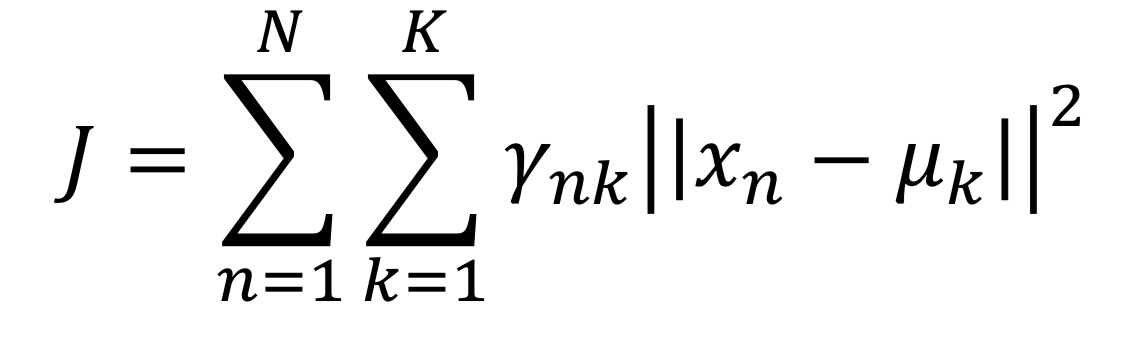
Algorithm (Lloyd/Forgy) [2]
- Initialize {𝜇1,...,𝜇𝐾} randomly (Usually selected as a random sample of the data points for faster convergence)
- Assignment Step (Minimization w.r.t. γ): Assign the indicator variable γij as 1 such that ith data point is closest to the jth cluster.
- Update Step (Minimization w.r.t. 𝜇): Update the centroid as the mean of the data points belonging to that cluster.
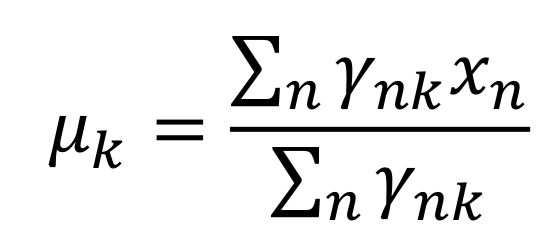
- If the model has not converged, repeat steps 2 and 3.
Convergence Model
The convergence of the model can be decided based on multiple measures, e.g.:
- The difference in cost function in subsequent iterations has reached some lower limiting value, e.g. 0.01 or something like that, this value is dependent on the input size and distance measure.
- The number of changes in point assignments has reached some lower limit.
- The number of iterations has reached some higher limit.
- Some other cluster quality metric, e.g. RAND index has reached some limit.
- And some more “hacky” ways sure exist in the system, which usually work based on the need.
Complexity of the Algorithm
O(NK) for each iteration
Going a little deep
The algorithm uses Euclidean distance as the distance metric and variance from the centroid is used as the objective function which we have to minimize. Because of the formulation, the algorithm forces to form what is generally called “spherical” clusters. These type of clusters are formed because the mean value of each cluster has to converge towards its centroid. The clusters are expected to be of similar size, so that the assignment to the nearest cluster center is the correct assignment. Another thing to be noted is that the clusters formed are “flat”, i.e. the clusters don’t have any relation among themselves. Algorithms like HAC provide clusters that are not flat. Other distance measures also used in place in the k means algorithm. The convergence is ensured for those metrics which can be “transformed” to euclidean distance. Cosine similarity is one such example.
The algorithm that we have described is a typical example of the EM algorithm. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step. In our algorithm, if euclidean distance is used, step 2 corresponds to the E step, and step 3 corresponds to the M step. The algorithm in our case is bound to converge to a local minimum if euclidean distance is used, but not necessary to the global minimum.
Things to take care of while implementing
There are two variables in the algorithm. First, you need to choose k. The choice of k in k-means, or even in FCM for that matter, is of utmost importance. Larger k will tend to split big clusters. If the dimensionality of the input is small then you can debug if k is large or not (i.e. the clusters are being split or not), but for higher dimensions the case is not so intuitive.
Second, you need to initialize the clusters. Random initialling works in most of the cases, but it might not always be the enough. The reason behind this is simple. If the initialisation is poor, it can converge to a local minima. The probability of this happening is more if the cluster structure in the input are not "easily separable”. The data is usually easily separable if the cluster structure includes “tight” clusters and the data is uniformly distributed among the clusters. Following is an animation of convergence to the global minimum (Image Source: simplystatistics.org).
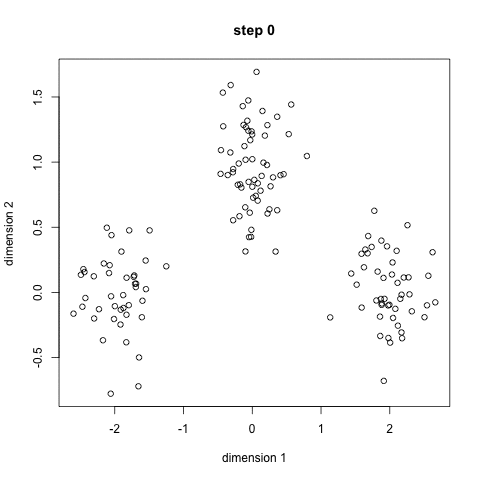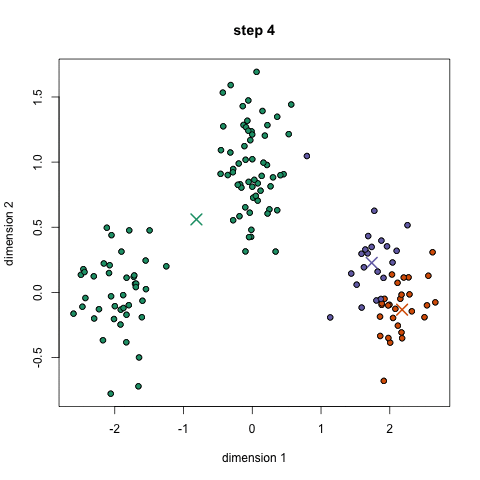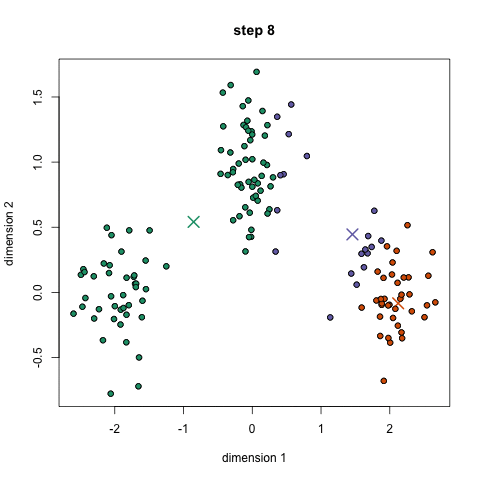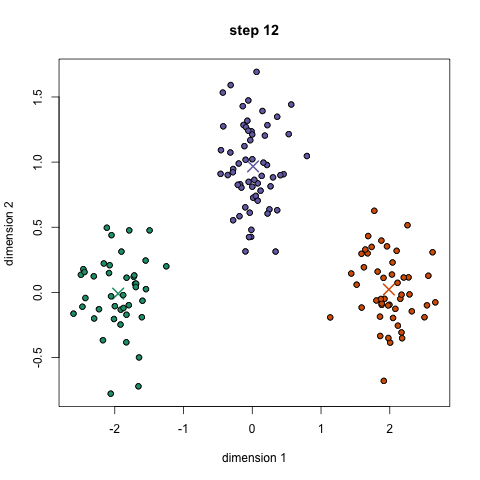
However, convergence to local minima is not that rare either. The following image for an example (Image Source: Wikipedia):
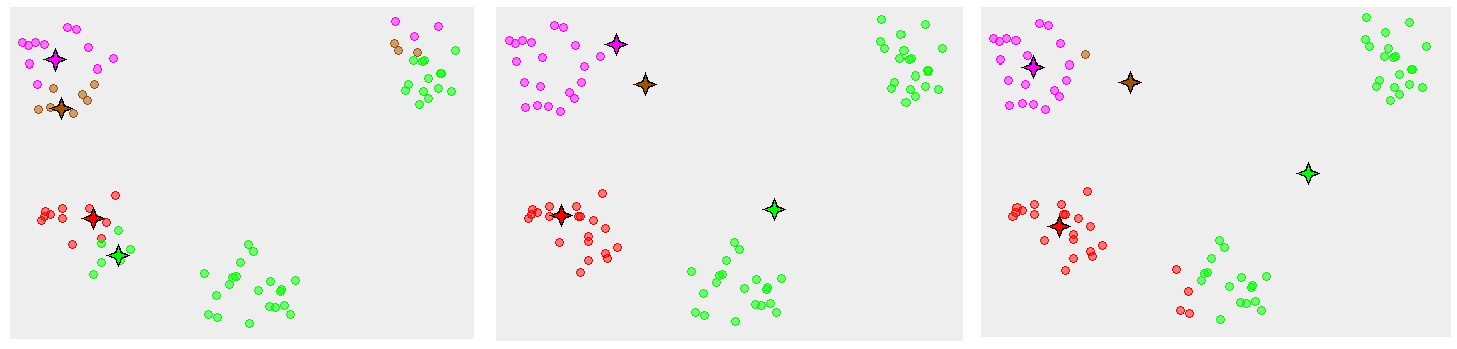
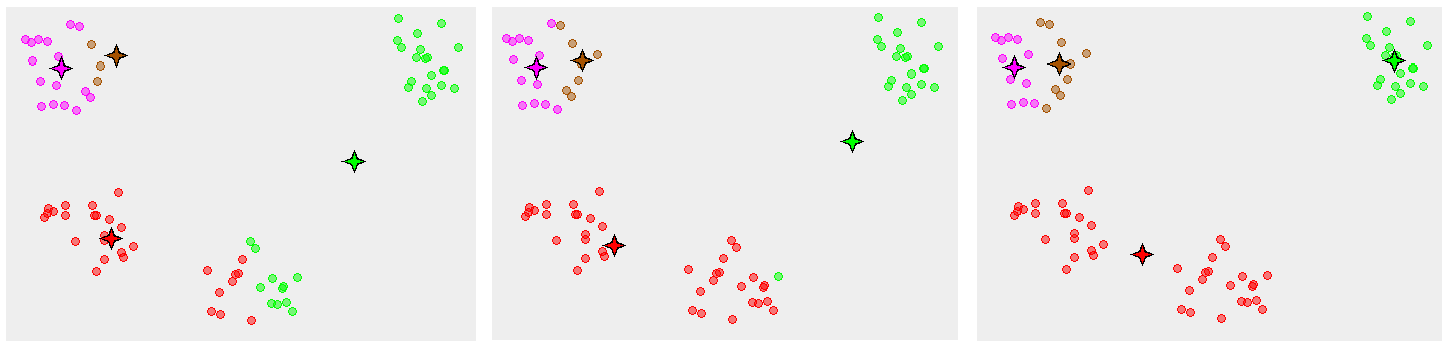
There have been works to a careful seeding. k-means++ [3] is an example reference.
There also exist a lot of variations to the k means algorithm, these algorithms together form a kind of family. One of the most popularly used alternative is the k-medoids algorithm.
References
- The Wikipedia Page for k-means clustering
- The Wikipedia Page for Lloyd's Algorithm
- Arthur, David, and Sergei Vassilvitskii. "k-means++: The advantages of careful seeding." Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics, 2007.